In the realm of crossword puzzles, the coordinate plane emerges as an indispensable tool, enabling solvers to pinpoint specific squares with precision. “There Are Two in a Coordinate Plane Crossword” delves into the intricate relationship between coordinate pairs and their role in deciphering these enigmatic grids.
Through a comprehensive exploration of the coordinate plane’s fundamentals, we uncover the significance of two points in determining distances and identifying the exact location of answers within a crossword puzzle.
Coordinate Plane Overview
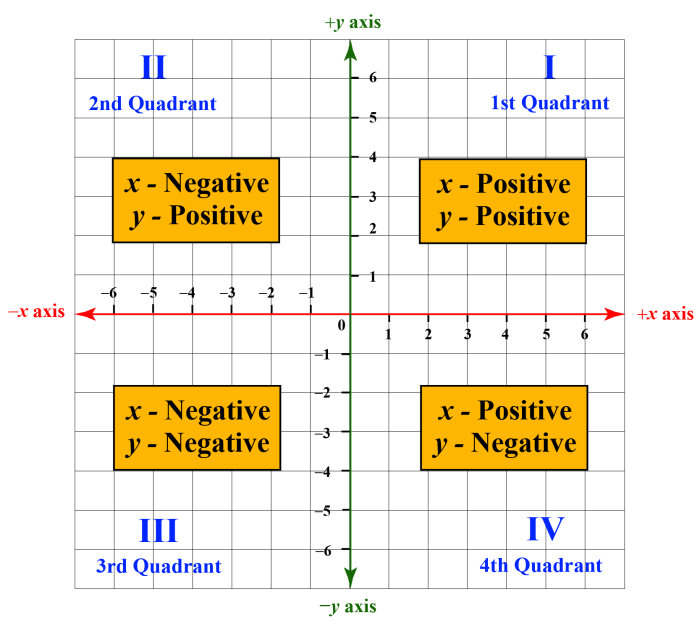
A coordinate plane is a two-dimensional space that is used to represent points and shapes. It consists of two perpendicular number lines, called the x-axis and the y-axis, which intersect at a point called the origin. The coordinate plane is divided into four quadrants, each of which is labeled with a Roman numeral (I, II, III, and IV).
Points on the coordinate plane are represented by ordered pairs of numbers (x, y), where x is the horizontal coordinate and y is the vertical coordinate. The x-coordinate tells us how far the point is to the right or left of the origin, and the y-coordinate tells us how far the point is above or below the origin.
For example, the point (3, 4) is located 3 units to the right of the origin and 4 units above the origin. It is located in quadrant I.
Two Points on a Coordinate Plane: There Are Two In A Coordinate Plane Crossword
Two points on a coordinate plane can be used to determine the distance between them using the distance formula.
The distance formula is:
d = √((x2
- x 1) 2+ (y 2
- y 1) 2)
where (x 1, y 1) and (x 2, y 2) are the coordinates of the two points.
For example, the distance between the points (3, 4) and (7, 10) is:
d = √((7
- 3)2+ (10
- 4) 2)
= √(16 + 36)= √52≈ 7.21
Coordinate Pair
A coordinate pair is an ordered pair of numbers (x, y) that represents a point on a coordinate plane. The first number in the pair is the x-coordinate, and the second number is the y-coordinate.
For example, the coordinate pair (3, 4) represents the point that is located 3 units to the right of the origin and 4 units above the origin.
Coordinate pairs are used to locate points on a coordinate plane. To plot a point on a coordinate plane, we start at the origin and move x units to the right or left, and then move y units up or down.
Plotting Points on a Coordinate Plane
To plot a point on a coordinate plane, we follow these steps:
- Start at the origin.
- Move x units to the right or left.
- Move y units up or down.
- The point is located at the intersection of the horizontal and vertical lines.
For example, to plot the point (3, 4), we start at the origin and move 3 units to the right and 4 units up. The point is located at the intersection of the horizontal line y = 4 and the vertical line x = 3.
Coordinate Plane in Crosswords
The coordinate plane is used in crossword puzzles to locate specific squares in the grid. Each square in the grid is assigned a coordinate pair, which consists of a letter and a number.
For example, the square in the top left corner of the grid is assigned the coordinate pair (A1). The square in the bottom right corner of the grid is assigned the coordinate pair (Z15).
To locate a square in a crossword grid using the coordinate plane, we simply find the letter and number that correspond to the square’s coordinate pair.
FAQ Overview
What is the significance of two points in a coordinate plane crossword puzzle?
Two points in a coordinate plane crossword puzzle establish a line segment, providing essential information for determining distances and locating specific squares within the grid.
How do I determine the distance between two points on a coordinate plane?
The distance formula, d = √((x2 – x1)² + (y2 – y1)²), calculates the distance between two points (x1, y1) and (x2, y2) on a coordinate plane.
How do coordinate pairs help me solve crossword puzzles?
Coordinate pairs translate crossword clues into specific locations on the grid. By plotting these pairs, solvers can pinpoint the corresponding squares where answers should be entered.
